Модель нормы остатка денежных средств

Нормирование остатка денежных средств предприятий позволяет осуществлять управление денежными потоками по отклонениям от установленной нормы. Достоинство данного подхода — его практическая направленность, то есть отсутствие сложного математического аппарата для принятия решений. При этом грамотно обоснованная и своевременно пересматриваемая норма остатка денежных средств позволяет принимать выверенные решения по управлению финансовыми ресурсами предприятия.

К сожалению, широко доступной литературы по нормированию оборотных средств в последнее время выходит мало. В качестве исключения можно указать, например, на фундаментальную работу [1]. Что же касается нормирования денежных средств, то данный вопрос вообще не находит внимания, соответствующего проблеме.

При этом знание финансовой службой предприятия обоснованной нормы денежных средств позволяет оперативно давать ответы на следующие вопросы: можно ли в сложившихся финансовых условиях осуществлять инвестиционные вложения в приобретение и строительство основных фондов? какую часть остатка денежных средств можно считать свободными и разместить их в качестве финансовых вложений? следует ли погасить задолженность по кредиту или целесообразно перекредитоваться?

В настоящей статье мы предлагаем модель нормы остатка денежных средств, основывающуюся на определении статистических закономерностей поступления и расхода денежных средств по операционной деятельности.

Основная идея предлагаемой модели состоит в том, что остаток денежных средств предприятия должен обеспечивать вместе с текущими поступлениями от операционной деятельности погашение задолженности по текущим обязательствам по операционной деятельности с заданной вероятностью.

Таким образом, статистические данные по движению денежных средств должны быть очищены от денежных потоков по инвестиционной и финансовой деятельности.

Напомним в связи с этим основы построения отчета о движении денежных средств.

Для составления отчета денежные средства разделяют на потоки от операционной, инвестиционной и финансовой деятельности (рис. 1).

Рис. 1. Общая классификация потоков денежных средств

Операционная деятельность — это основная деятельность предприятия, которая приносит доход и не является инвестиционной или финансовой деятельностью.

Примерами потоков денежных средств от операционной деятельности служат поступления денежных средств от продажи продукции, потребления сырья и материалов, выплата заработной платы, оплата операционных расходов, уплата налогов, поступления и выплаты денежных средств, связанные с продажей и покупкой ценных бумаг, предназначенных для перепродажи, и др.

Инвестиционная деятельность связана с приобретением и ликвидацией необоротных активов и других инвестиций, которые не относятся к эквивалентам денежных средств и к инвестициям, предназначенным для перепродажи.

В качестве примеров потоков денежных средств от инвестиционной деятельности можно привести оплату приобретенных основных средств, нематериальных активов, долгосрочных инвестиций, денежные средства, полученные от реализации основных средств и других необоротных активов, займы, предоставленные другим предприятиям, возврат таких займов и др.

Финансовая деятельность — это деятельность, результатом которой являются изменения в величине, составе собственного капитала и заемных средств предприятия.

Примерами потоков денежных средств от финансовой деятельности являются поступления денежных средств от выпуска акций, выплаты денежных средств, связанные с выкупом акций, получение и возврат кредитов, поступления денежных средств от выпуска облигаций, выплаты денежных средств, связанные с погашением облигаций, и др.

Один из неоднозначно решаемых вопросов — вопрос классификации процентов и дивидендов. Проблема состоит в том, что выплаченные и полученные проценты и дивиденды могут быть классифицированы и как операционная (поскольку связаны с текущей хозяйственной деятельностью), и как инвестиционная (поскольку полученные проценты и дивиденды являются результатом инвестиций), и как финансовая (поскольку выплаченные проценты и дивиденды являются результатом привлечения источников финансирования) деятельность.

Международные стандарты разрешают классифицировать полученные и выплаченные проценты и дивиденды любым способом при условии, что выбранная классификация будет использоваться на постоянной основе.

Мы примем, что выплаченные дивиденды относятся к расходам по финансовой деятельности.

Сейчас перейдем к вопросу формирования информационной базы исследования.

Бухгалтерские данные о ежедневном поступлении денежных средств за выбранный для исследования период, например за предшествующий финансовый год, следует очистить от поступлений от инвестиционной и финансовой деятельности. Какой период времени использовать — это отдельная тема. Здесь же заметим лишь то, что данные о поступлении денежных средств должны быть сопоставимы. Это значит, что инфляция за выбранный для анализа период должна быть умеренной (полагаем, что можно говорить о пороге 10–12 %). Кроме того, в деятельности предприятия за анализируемый период не должно происходить каких-либо качественных изменений, например выхода на новые рынки сбыта и т.п.

Для анализа оттока денежных средств нельзя брать бухгалтерские данные о фактически произведенных расходах по операционной деятельности. Следует использовать данные о возникновении обязательств. В принципе, бухгалтерские данные для наших целей вообще мало пригодны. Действительно, метод двойной записи не предполагает, например, отражения задолженности, возникающей по обязательствам предоплаты за сырье, материалы. Желательно в финансовой службе предприятия иметь собственную базу данных о состоянии расчетов с контрагентами, где отражать данные обо всех возникших обязательствах, причем с разбивкой на обязательства возникшие, но срок исполнения которых еще не наступил, и, соответственно, по обязательствам с наступившим сроком исполнения. В крайнем случае можно использовать бухгалтерские данные, но не по движению денег с расчетных, валютных счетов и кассы, а по оборотам возникновения кредиторской задолженности. Причем нужны ежедневные данные. Они также должны быть очищены от кредиторской задолженности по инвестиционной и финансовой деятельности.

Итак, пусть информационная база исследования сформирована. Перейдем сейчас к описанию математической модели нормирования денежных средств.

Определим приток денежных средств от операционной деятельности посредством случайной величины X, а отток денежных средств от операционной деятельности — посредством случайной величины Y. Припишем случайной величине X знак минус.

Введем случайную величину Z = X + Y.

Таким образом, Z > 0 при недостатке поступающих денежных средств для удовлетворения требования кредиторов (поставщиков, бюджета и внебюджетных фондов и т.п.) и Z < 0, если поступающих денежных средств от операционной деятельности избыточно для погашения текущих обязательств, связанных с операционной деятельностью предприятия.

Предположим, что величины X и Y подчиняются нормальному закону распределения вероятностей, что в большинстве практических ситуаций недалеко от истины. Тогда величина Z также является нормально распределенной.

Справка

Анализ общих условий возникновения нормального распределения показывает, что наиболее важным условием выступает формирование признака как суммы большого числа взаимно независимых слагаемых, ни одно из которых не характеризуется исключительно большой по сравнению с другими дисперсией. Главная особенность нормального распределения состоит в том, что оно является предельным, к которому приближаются другие распределения.

Термин «нормальное распределение» применяется в условном смысле как общепринятый в литературе. Так, утверждение, что какой-то признак подчиняется нормальному закону, вовсе не означает наличие каких-то незыблемых норм, якобы лежащих в основе явления, отражением которого является рассматриваемый признак, а подчинение другим видам законов не означает какую-то аномальность данного явления.

Распределение совокупности значений по нормальному закону может быть задано в виде следующей аналитической функции распределения:

                                                            (1)

     F(z) называется интегральной функцией распределения, а f(z) — дифференциальной функцией распределения случайной величины (иной термин — функция плотности распределения). В нашем случае такой случайной величиной является Z — разница между оттоком и поступлением денежных средств. Заметим, что интегральная функция нормального распределения не имеет выражения через известные математические функции, поэтому она представляется через интеграл дифференциальной функции.

График плотности нормального распределения называют нормальной кривой. Она представляет собой колоколообразную фигуру, симметричную относительно прямой, проходящей через точку z = a и в пределе приближающуюся к оси абсцисс при z → ±∞.

Если X и Y являются нормально распределенными случайными величинами, то сумма Z = X + Y есть также нормально распределенная случайная величина [2, с. 797–798] с параметрами:

                        MZ = a₁ + a₂,                                               (2)

                                                                        (3)

где MZ — математическое ожидание случайной величины Z;

a₁ — математическое ожидание случайной величины X;

a₂ — математическое ожидание случайной величины Y;

σ — стандартное отклонение случайной величины Z;

σ₁ — стандартное отклонение случайной величины X;

σ₂ — стандартное отклонение случайной величины Y;

r — коэффициент корреляции X и Y.

Итак, вероятность попадания случайной нормально распределенной величины Z (в нашем случае — избытка или недостатка поступления денег для текущих расходов) в интервал [–∞, β] равна значению интегральной функции (1) при z = β.

Значение β cверху ограничено значением максимальной разницы между оттоком и поступлением денежных средств. Очевидно, что при таком остатке денежных средств проблемы с погашением текущих обязательств не существовало бы вовсе. При этом необходимо иметь в виду, что обеспечение остатка денежных средств, гарантирующего на 100 % погашение возникновения абсолютно всех текущих обязательств только собственными денежными средствами, чрезвычайно расточительно для любого предприятия. Любой финансовый менеджер предпримет усилия для отсрочки платежа, если это возможно, постарается найти зачетные схемы исполнения обязательств, включая выпуск собственных векселей, и т.п.

Задавшись значением вероятности обеспечения оплаты по текущим обязательствам (P) можно решить обратную задачу, а именно, каковым должен быть показатель β для заданной вероятности. Значение данного показателя β и будет являться решением задачи об определении уровня неснижаемого остатка денежных средств, с заданной вероятностью обеспечивающего погашение текущих обязательств.

Для практической работы с нормальным распределением вероятностей нет необходимости вникать в относительно сложный математический аппарат. В Microsoft Excel, например, имеются все необходимые встроенные функции, чтобы обеспечить расчеты. Так функция НОРМОБР() позволяет получить значение случайной нормально распределенной величины, соответствующее заданному значению вероятности.

Как мы уже указывали выше, выбор значения P, отличного от единицы, позволяет учесть иные способы погашения обязательств перед кредиторами, чем оплата собственными денежными средствами, а именно: зачетные (вексельные) схемы, пополнение оборотных средств за счет привлечения кредитов, займов. Иными словами, если, например, за счет зачетных схем предполагается погашать до 25 % всей образующейся текущей кредиторской задолженности, то значение P следует установить на уровне 0,75. Кроме того, показатель вероятности погашения текущих обязательств является одним из элементов, характеризующих риск финансово-хозяйственной деятельности в условиях недетерминированной экономики. Поэтому на выбор конкретного значения данного показателя оказывает влияние помимо объективных факторов и ментальность руководителя финансовой службы предприятия — его интуиция и склонность к риску.

Если величина Z не соответствует нормальному закону распределения вероятностей или какому-либо иному известному закону, выражаемому посредством аналитических функций, то решить рассматриваемую нами задачу можно путем построения эмпирической функции распределения вероятностей для Z [4, с. 381–383, 538–539]. Построение эмпирической функции распределения вероятностей величины Z не предполагает никаких гипотез о виде (аналитической формуле) функции распределения вероятностей. Геометрически она представляет  собой совокупность отрезков. Иначе говорят, что эмпирическая функция распределения вероятностей является кусочно-линейной.

Данная функция может быть определена как для отдельных исходных наблюдений Z₁, Z₂, …, Z_n, так и для сгруппированных данных. Мы рассмотрим второй случай.

Предположим, что n величины Z_i сгруппированы в k смежных интервалов [a₀, a₁), [a₁, a₂), …, [a_{k – 1}, a_k) так, чтобы j-й интервал содержал n_j наблюдений, где n₁ + n₂ + … + n_k = n. Обозначим функцию через G. Положим, что G(a₀) = 0 и G(a_j) = (n₁ + n₂ + … + n_j) / n для j = 1, 2, …, k. Тогда G определяется для любого значения z следующим образом:

G(z)= 0, если z < a₀;

если a_j-1 ≤ z <a_j  для a =1, 2, …, k;                                 (4)

G(z) = 1, если a_k < z.

Диаграмма функции G(z) представлена ниже.

Данную функцию несложно программировать. Пример пользовательской функции, написанной на VBA для Microsoft Excel, приведен ниже.

Function x3emp(P, A1, H, ParamArray OA()) As Double

'Описание передаваемых переменных

'   P - вероятность

'   A1 - начало первого интервала

'   H - интервал

'   OA() - массив, содержащий частоты

Dim G(64) As Double ' Накопленная частота

Dim Interval(64) As Double ' Интервалы частот

Dim sum_fr As Double ' Сумма частот

n = UBound(OA()) + 1

'---------- считаем сумму частот ---------------------------------------------

sum_fr = 0

For i = 0 To n - 1

   sum_fr = sum_fr + OA(i)

Next i

'---------- разбор массива частот --------------------------------------------

Interval(0) = A1 - H / 2

G(0) = 0

For i = 0 To n - 1

    Interval(i + 1) = Interval(i) + H

    G(i + 1) = G(i) + OA(i) / sum_fr

Next i

'---------- позиционируемся в массиве G и возвращаем искомое значение ---------

For i = 0 To n - 1

    If G(i) <= P And P <= G(i + 1) Then

       x3emp = Interval(i) + (P - G(i)) * (Interval(i + 1) - Interval(i)) / (G(i + 1) - G(i))

       Exit Function

    End If

Next i

End Function

Прежде чем рассмотреть пример, резонно задать вопрос: «Хорошо, норма неснижаемого остатка денежных средств определена, но в настоящий период предприятие не имеет на счетах такой суммы. Как ее обеспечить?»

Если возникающие текущие обязательства превышают входящий денежный поток от операционной деятельности, то задача не имеет решения — предприятие уверенно идет к банкротству, если только систематически не практикуются зачетные схемы погашения задолженности.

Замечание

Привлечение заемных средств может в этом случае дать лишь кратковременный эффект, а в дальнейшем ситуация усугубится. Очевидно, что заемные средства целесообразно систематически привлекать только в том случае, если они будут способствовать улучшению финансовой ситуации путем расширения рынков сбыта, увеличения рентабельности продаж. Статистический подход к нормированию остатка денежных средств в этом случае не применим. Вместо фактических данных о движении денежных средств и кредиторской задолженности в такой ситуации необходимо использовать для моделирования прогнозные данные по бизнес-плану.

В ином случае накопить соответствующий остаток денежных средств возможно путем активизации работы по взысканию дебиторской задолженности покупателей, сокращения (временного прекращения) финансирования инвестиционных проектов и иных расходов по финансовой деятельности, получения отсрочек по кредитам и/или перекредитования. Как факультативную возможность следует рассматривать дополнительные вложения собственников в имущество предприятия (исключая, очевидно, открытые акционерные общества). Получение новых заемных средств для доведения остатка денежных средств до нормативного остатка представляется неверным, так как вызовет лишь неоправданные новые расходы на обслуживание кредитов.

Теперь несколько замечаний о «неснижаемости» остатка. В действительности это не совсем так. В течение нескольких дней вполне возможно временное уменьшение остатка ниже нормативного уровня. Действительно, решаемая нами задача не является детерминированной. Важно лишь руководствоваться правилом: финансирование инвестиционной и финансовой деятельности (включая возврат заемных средств) возможно только из разницы фактического остатка денежных средств на счетах и его нормативного уровня.

Пример

Предлагаемый пример расчета нормы остатка денежных средств основан на реальных данных предприятия за 2005 г., которое по показателям его финансово-хозяйственной деятельности можно отнести к средним в своем сегменте бизнеса.

Информационная база исследования включала данные в следующем формате (табл. 1).

Таблица 1. Данные о поступлении и оттоке денежных средств по операционной деятельности (фрагмент)

Данные были получены из базы данных финансового (бухгалтерского) учета. Как мы уже указывали выше, данными из этого источника следует пользоваться с осторожностью. Но для целей иллюстративного примера, как мы полагаем, такие данные вполне подойдут.

При этом мы дополнительно очистили исходные данные от внутренних «перебросок» кредиторской задолженности по счетам расчетов (поставщики, прочие кредиторы, задолженность перед бюджетом и внебюджетными фондами), которые могут исказить (необоснованно увеличить) действительный объем возникающих обязательств.

Из информационной базы были исключены также данные по тем датам, когда поступление денежных средств и возникновение обязательств отсутствовали.

Для группировки данных сальдо поступления денежных средств и возникновения текущих обязательств была использована формула Стэрджеса [3, с. 18]:

h = (Z_max – Z_min) / (1 + 3,322lg n),                                                                   (5)

где h — оптимальный интервал;

Z_max — максимальное значение разницы между оттоком и поступлением денежных средств,

Z_min — минимальное значение разницы между оттоком и поступлением денежных средств;

n — количество строк (наблюдений) в табл. 1.

В нашем случае Z_min = –24 095 855,50 руб., Z_max = 10 469 885,34 руб. и n = 254.

За начало первого интервала рекомендуется принимать величину a₁ = Z_min – h / 2, начало второго интервала совпадает с концом первого и равно a₂ = a₁ + h, начало третьего интервала совпадает с концом второго и равно a₃ = a₂ + h. Построение интервалов продолжаем до тех пор, пока начало следующего по порядку интервала не будет больше Z_max. После установления шкалы интервалов следует сгруппировать результаты наблюдений.

Используя программу Microsoft Excel, группировку результатов наблюдений легко выполнить при помощи функции ЧАСТОТА().

Для нашей информационной базы результаты расчетов, выполненные при помощи  данной функции, представлены в табл. 2.

Таблица 2. Сгруппированные данные о поступлении и оттоке денежных средств по операционной деятельности

Эмпирическая функция распределения вероятностей для рассматриваемого примера приведена на рис. 2. Аргументом данной функции является случайная величина Z, равная разнице возникновения текущих обязательств и поступления денежных средств от операционной деятельности за календарный день. Значение рассматриваемой функции F(z₀) = P(Z < z₀) определяет вероятность того, что случайная величина Z примет значение меньше фиксированного числа z₀. Таким образом, значение z₀ представляет собой остаток денежных средств, который обеспечивает погашение возникающих денежных обязательств с вероятностью F(z₀). Функция F(z₀) называется также интегральной функцией распределения вероятностей .

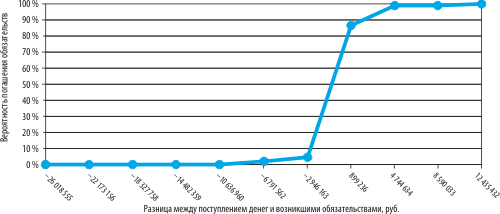
Рис. 2. Эмпирическая функция распределения вероятностей для рассматриваемого примера

Таблица 3. Норма остатка денежных средств в зависимости от вероятности погашения обязательств

Выбор конкретной нормы остатка денежных средств остается за руководителем финансовой службы предприятия.

Мы должны лишь заметить, что предприятие, данные которого были использованы для примера, имело на расчетных счетах в 2005 г. среднедневной остаток 818 670,78 руб., что позволяет погашать текущие обязательства за счет собственных средств с вероятностью около 85 %. Полученные данные свидетельствуют о нормальной финансовой ситуации на предприятии, если принимать во внимание то, что предприятие практикует зачетные схемы погашения обязательств.

Полагаем, что предложенная нами модель определения нормы остатка денежных средств позволит снизить расходы на привлечение кредитных ресурсов для покрытия кассовых разрывов, а также грамотно планировать денежные потоки, включая инвестиционные вложения в основные средства, выплату дивидендов, иное размещение свободных денежных средств. Выверенные управленческие решения в части регулирования денежных потоков — это один из самых эффективных способов улучшения финансового состояния предприятия.